Strukturen, die von ganzzahligen irreduziblen Polynomen 3. Grades erzeugt werden
Polynome 3. Grades:
Jedes Polynom 3. Grades kann durch eine TSCHIRNHAUS-Transformation
vom quadratischen Term befreit werden.
(Solche Transformationen wurden erstmals systematisch von
Graf Ehrenfried Walter von TSCHIRNHAUSEN
aus Kieslingswalde bey Görlitz untersucht.)
Es ist also keine Einschränkung der Allgemeinheit, wenn wir annehmen,
das Polynom habe die Normalform P(X) = X3 + CX + D mit ganz rationalen Koeffizienten C und D.
Eine Nullstelle xi eines über dem Körper Q der rationalen Zahlen irreduziblen Polynoms 3. Grades
erzeugt durch Adjunktion an Q einen kubischen Zahlkörper L = Q(xi).
Nach der Anzahl der reellen Nullstellen des erzeugenden Polynomes P(X) unterscheiden wir
einfach reelle (oder komplexe) kubische Körper und
dreifach (oder total) reelle kubische Körper.
1. Einfach reelle kubische Körper
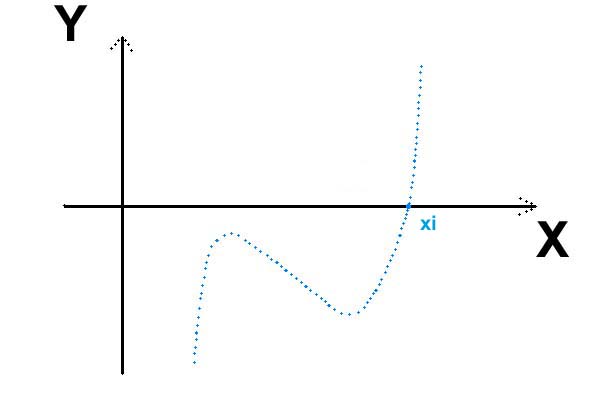 P(X) besitzt über R eine Zerlegung
P(X) = (X - xi) (X2 + beta X + gamma)
mit der reellen Nullstelle xi in R
und einem über R irreduziblen Polynom 2. Grades mit Koeffizienten beta,gamma in R.
Erst über C spaltet dieser quadratische Faktor weiter auf in
(X - xi') (X - xi'')
mit den konjugiert komplexen Nullstellen xi',xi'' in C.
Der reelle kubische Zahlkörper
L = Q(xi)
besitzt zwei konjugierte, isomorphe komplexe kubische Zahlkörper
L' = Q(xi') und L'' = Q(xi'').
Die Körper-Monomorphismen von L gliedern sich in
eine reelle Inklusion
L-->R, xi-->xi
und ein Paar von konjugiert komplexen Einbettungen
L-->C, xi-->xi',
L-->C, xi-->xi''.
Die Signatur (s,t) von L,
wobei s die Anzahl der reellen Einbettungen
und t die Anzahl der Paare von konjugiert komplexen Einbettungen bedeutet,
ist also (1,1).
Der Einheitensatz von Dirichlet zeigt daher,
dass die Einheitengruppe U_L von L
durch eine einzige Fundamentaleinheit e (unendlicher Ordnung)
und die Einheitswurzel -1
erzeugt werden kann: U_L = < e, -1 >.
P(X) besitzt über R eine Zerlegung
P(X) = (X - xi) (X2 + beta X + gamma)
mit der reellen Nullstelle xi in R
und einem über R irreduziblen Polynom 2. Grades mit Koeffizienten beta,gamma in R.
Erst über C spaltet dieser quadratische Faktor weiter auf in
(X - xi') (X - xi'')
mit den konjugiert komplexen Nullstellen xi',xi'' in C.
Der reelle kubische Zahlkörper
L = Q(xi)
besitzt zwei konjugierte, isomorphe komplexe kubische Zahlkörper
L' = Q(xi') und L'' = Q(xi'').
Die Körper-Monomorphismen von L gliedern sich in
eine reelle Inklusion
L-->R, xi-->xi
und ein Paar von konjugiert komplexen Einbettungen
L-->C, xi-->xi',
L-->C, xi-->xi''.
Die Signatur (s,t) von L,
wobei s die Anzahl der reellen Einbettungen
und t die Anzahl der Paare von konjugiert komplexen Einbettungen bedeutet,
ist also (1,1).
Der Einheitensatz von Dirichlet zeigt daher,
dass die Einheitengruppe U_L von L
durch eine einzige Fundamentaleinheit e (unendlicher Ordnung)
und die Einheitswurzel -1
erzeugt werden kann: U_L = < e, -1 >.
2. Dreifach reelle kubische Körper
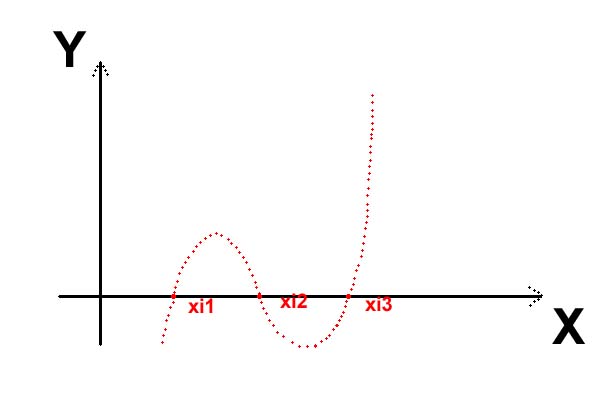 P(X) zerfällt über R vollständig in Linearfaktoren
P(X) = (X - xi1) (X - xi2)(X - xi3)
mit den drei reellen Nullstellen xi1,xi2,xi3 in R.
Die drei Nullstellen erzeugen drei konjugierte, isomorphe reelle kubische Zahlkörper
L1 = Q(xi1),
L2 = Q(xi2),
L3 = Q(xi3).
An Körper-Monomorphismen von L1 haben wir
die reelle Inklusion
L1-->R, xi1-->xi1
und die reellen Einbettungen
L1-->R, xi1-->xi2,
L1-->R, xi1-->xi3.
Dementsprechend ergibt sich für die Signatur von L1
(s,t) = (3,0).
Gemäß dem Einheitensatz von Dirichlet
besitzt die Einheitengruppe U_L von L in diesem Fall
ein Fundamentalsystem aus genau 2 Einheiten e_1 und e_2 (unendlicher Ordnung)
und der Einheitswurzel -1:
U_L = < e_1, e_2, -1 >.
P(X) zerfällt über R vollständig in Linearfaktoren
P(X) = (X - xi1) (X - xi2)(X - xi3)
mit den drei reellen Nullstellen xi1,xi2,xi3 in R.
Die drei Nullstellen erzeugen drei konjugierte, isomorphe reelle kubische Zahlkörper
L1 = Q(xi1),
L2 = Q(xi2),
L3 = Q(xi3).
An Körper-Monomorphismen von L1 haben wir
die reelle Inklusion
L1-->R, xi1-->xi1
und die reellen Einbettungen
L1-->R, xi1-->xi2,
L1-->R, xi1-->xi3.
Dementsprechend ergibt sich für die Signatur von L1
(s,t) = (3,0).
Gemäß dem Einheitensatz von Dirichlet
besitzt die Einheitengruppe U_L von L in diesem Fall
ein Fundamentalsystem aus genau 2 Einheiten e_1 und e_2 (unendlicher Ordnung)
und der Einheitswurzel -1:
U_L = < e_1, e_2, -1 >.
DIRICHLETscher Einheitenrang
Wie jede ABELsche Gruppe läßt sich auch
die Einheitengruppe U_K eines algebraischen Zahlkörpers K
in das direkte Produkt des Anteils endlicher Ordnung und des Anteils unendlicher Ordnung
zerlegen.
Der Anteil endlicher Ordnung heißt allgemein die Torsionsuntergruppe
und hier speziell die Untergruppe der Einheitswurzeln oder Torsionseinheiten TU_K.
Unter dem DIRICHLETschen Einheitenrang r versteht man
die Anzahl der freien Erzeugenden unendlicher Ordnung,
also den Z-Rang des torsionsfreien Anteils.
Der fundamentale DIRICHLETsche Einheitensatz besagt,
dass sich der DIRICHLETsche Einheitenrang r in der folgenden Weise
aus der Signatur (s,t) berechnen läßt:
r = s + t - 1.
(Die Signatur ist mit dem absoluten Grad n = [K:Q] von K
durch die Beziehung s + 2t = n verbunden.)
TSCHIRNHAUS-Transformationen
Im allgemeinsten Fall verstehen wir unter einer TSCHIRNHAUS-Transformation die Abbildung,
die jedem Element rho eines algebraischen Zahlkörpers L das Hauptpolynom H_rho(X) von rho
zuordnet:
L --> Q[X], rho --> H_rho(X) = det( X*1_L - h_rho )
wobei h_rho in End_Q(L) die Homothetie alpha --> rho * alpha bedeutet.
Die TSCHIRNHAUS-Transformation ist von der Wahl einer Q-Basis von L unabhängig.
Insbesondere wird sie nicht beeinflusst
von der Auswahl eines primitiven Elementes delta von L = Q( delta ) mit zugehöriger Potenzbasis
(1,delta,...,deltan-1), wobei n den Grad [L:Q] von L über Q bezeichnet.
Für die konkrete Berechnung wählen wir allerdings ein primitives Element delta von L
und erhalten dann den Eindruck, die TSCHIRNHAUS-Transformation
führe das Minimalpolynom M_delta(X) von delta in das Hauptpolynom H_rho(X) von rho über:
L * { P(X) in Q[X] | P normiert und irreduzibel vom Grad n } --> Q[X], ( rho, M_delta(X) ) --> H_rho(X)
wobei rho = r0 + r1*delta + ... + rn-1*deltan-1,
weil L = Q + Q*delta + ... + Q*deltan-1 als Q-Vektorraum,
und M_delta(X) = Xn + Mn-1*Xn-1 + ... + M1*X + M0
sowie H_rho(X) = Xn + Hn-1*Xn-1 + ... + H1*X + H0.
Die Koeffizienten Hi des Hauptpolynoms H_rho(X) erscheinen als Polynome in den
Koordinaten ri von rho bezüglich delta
und in den Koeffizienten Mi des Minimalpolynoms M_delta(X).
Zurück zur
Startseite von Daniel C. Mayer.
 P(X) besitzt über R eine Zerlegung
P(X) = (X - xi) (X2 + beta X + gamma)
mit der reellen Nullstelle xi in R
und einem über R irreduziblen Polynom 2. Grades mit Koeffizienten beta,gamma in R.
Erst über C spaltet dieser quadratische Faktor weiter auf in
(X - xi') (X - xi'')
mit den konjugiert komplexen Nullstellen xi',xi'' in C.
Der reelle kubische Zahlkörper
L = Q(xi)
besitzt zwei konjugierte, isomorphe komplexe kubische Zahlkörper
L' = Q(xi') und L'' = Q(xi'').
Die Körper-Monomorphismen von L gliedern sich in
eine reelle Inklusion
L-->R, xi-->xi
und ein Paar von konjugiert komplexen Einbettungen
L-->C, xi-->xi',
L-->C, xi-->xi''.
Die Signatur (s,t) von L,
wobei s die Anzahl der reellen Einbettungen
und t die Anzahl der Paare von konjugiert komplexen Einbettungen bedeutet,
ist also (1,1).
Der Einheitensatz von Dirichlet zeigt daher,
dass die Einheitengruppe U_L von L
durch eine einzige Fundamentaleinheit e (unendlicher Ordnung)
und die Einheitswurzel -1
erzeugt werden kann: U_L = < e, -1 >.
P(X) besitzt über R eine Zerlegung
P(X) = (X - xi) (X2 + beta X + gamma)
mit der reellen Nullstelle xi in R
und einem über R irreduziblen Polynom 2. Grades mit Koeffizienten beta,gamma in R.
Erst über C spaltet dieser quadratische Faktor weiter auf in
(X - xi') (X - xi'')
mit den konjugiert komplexen Nullstellen xi',xi'' in C.
Der reelle kubische Zahlkörper
L = Q(xi)
besitzt zwei konjugierte, isomorphe komplexe kubische Zahlkörper
L' = Q(xi') und L'' = Q(xi'').
Die Körper-Monomorphismen von L gliedern sich in
eine reelle Inklusion
L-->R, xi-->xi
und ein Paar von konjugiert komplexen Einbettungen
L-->C, xi-->xi',
L-->C, xi-->xi''.
Die Signatur (s,t) von L,
wobei s die Anzahl der reellen Einbettungen
und t die Anzahl der Paare von konjugiert komplexen Einbettungen bedeutet,
ist also (1,1).
Der Einheitensatz von Dirichlet zeigt daher,
dass die Einheitengruppe U_L von L
durch eine einzige Fundamentaleinheit e (unendlicher Ordnung)
und die Einheitswurzel -1
erzeugt werden kann: U_L = < e, -1 >.
 P(X) zerfällt über R vollständig in Linearfaktoren
P(X) = (X - xi1) (X - xi2)(X - xi3)
mit den drei reellen Nullstellen xi1,xi2,xi3 in R.
Die drei Nullstellen erzeugen drei konjugierte, isomorphe reelle kubische Zahlkörper
L1 = Q(xi1),
L2 = Q(xi2),
L3 = Q(xi3).
An Körper-Monomorphismen von L1 haben wir
die reelle Inklusion
L1-->R, xi1-->xi1
und die reellen Einbettungen
L1-->R, xi1-->xi2,
L1-->R, xi1-->xi3.
Dementsprechend ergibt sich für die Signatur von L1
(s,t) = (3,0).
Gemäß dem
P(X) zerfällt über R vollständig in Linearfaktoren
P(X) = (X - xi1) (X - xi2)(X - xi3)
mit den drei reellen Nullstellen xi1,xi2,xi3 in R.
Die drei Nullstellen erzeugen drei konjugierte, isomorphe reelle kubische Zahlkörper
L1 = Q(xi1),
L2 = Q(xi2),
L3 = Q(xi3).
An Körper-Monomorphismen von L1 haben wir
die reelle Inklusion
L1-->R, xi1-->xi1
und die reellen Einbettungen
L1-->R, xi1-->xi2,
L1-->R, xi1-->xi3.
Dementsprechend ergibt sich für die Signatur von L1
(s,t) = (3,0).
Gemäß dem